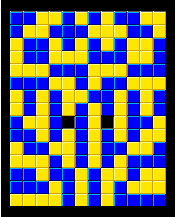


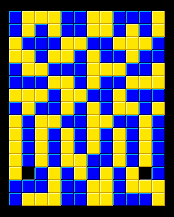
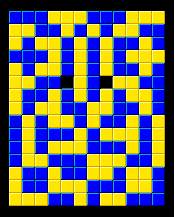



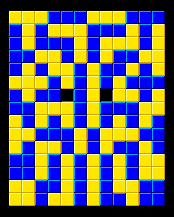




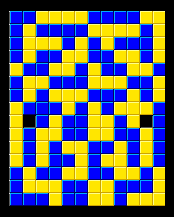


| Blokus Puzzles: 2 Colors 12x15 | Home | Blokus Discoveries | Send Your Feedback |
Presented below are 15 different solutions with two colors, with only corner-touching of the same color, and all pieces of each color in one continuous chain, on a 12x15 board. There are only two empty squares, always adjoining the I-pentomino, which, with its sides of 5 cannot be completely covered. One of its long sides always lies along an edge or the other I-pentomino, and one square along the other long side is left empty.
All of these were found by computer and are based on symmetric halves. In all cases but two (the first and the last), the two halves can be exchanged across the vertical central axis to produce another solution.
In both of the exceptional cases, the Monomino would be left in isolation, touching no other piece if the halves were swapped.
The first 14 solutions are presented based on the location of the uppermost square of the X pentomino in (x,y) coordinates, with the upper left being (0,0). It can be placed anywhere EXCEPT surrounding one of the outer corners. The last solution shown has the I pentonimo parallel to the short side, in the only such position it can be placed.
It may be possible to find an asymmetric solution, perhaps even with one I-pentomino along an edge and the other next to it, but that would be a very difficult task.
On another page, 15 other solutions in the same vein are shown. These are 10x18, created out of two 10x9 halves. One position of the X pentomino had no such solutions. One of them is solvable in size-descending order: all the pentominoes can be placed first, then the tetrominoes, triominoes, domino, and finally the monomino. All of them can have their halves swapped to form new solutions.
And on a third page, 17 other solutions for a slightly larger rectangle, 13x14 (2 more squares than the other two). In that case, the X can go anywhere except surrounding the corner, (a case which wasn't tried), and the I lays along the edge of one of the halves, in any position on the 13 side, or in the corner on of one of the halves on the 14 side.
X 0,4 not 1 |
X 0,2 or 3 |
X 1,1 or 4 |
X 1,2 or 3 |
X 2,1 or 4 |
X 2,2 or 3 |
X 3,1 or 4 |
X 3,2 or 3 |
X 4,1 or 4 |
X 4,2 or 3 |
X 5,1 or 4 |
X 5,2 or 3 |
X 6,1 or 4 |
X 6,2 or 3 |
I (horiz) 0,0 |